2019年度「プログラミング言語」配布資料 (8)

五十嵐 淳 (京都大学大学院情報学研究科 通信情報システム専攻)

2019年11月15日

[ 前の資料 | 講義ホームページ・トップ | 次の資料 ]

再帰と繰り返し

while や for などの 繰り返し(iteration) の構文を使いこなすことは，プログラミング，特にJava(やC言語)でのプログラミングにおいては必須の技術である．しかしながら，本稿では，不自然と思えるくらいに繰り返し構文を使っていない．その理由としては以下のようなことがあげられる．

本章では，「何度も同じような計算を行う」ための手法である再帰と繰り返しを比較していく．

メソッド・関数呼出しとフレーム

ここで，関数やメソッド呼出しの仕組みを一旦説明しておく．

Java の場合

配布資料その(1)(「メソッド呼出し」以降)に書きました．

OCaml の場合

OCaml では，変数の値の情報は「フレーム」ではなく 環境(environment) と呼ぶ．以下，プログラムの実行過程(式の評価過程)を，環境を使って説明する．max_int など，最初から使える変数は起動時の環境(トップレベル環境)に定義されていると考えられる．

let宣言 (let\(x\)=\(e\);;)
トップレベル環境を使って式\(e\)の値 \(v\) を求める．その後トップレベル環境に，\(x\) = \(v\) という変数束縛を付加したものが次の入力を処理する時の環境となる．なお，環境に同じ名前の変数が既に現れている場合でも，古い関連づけはそのままで新しい関連づけを追加する．
let式 (let\(x\)=\(e_1\)in\(e_2\))
現在の環境を使って式 \(e_1\) の値 \(v_1\) を求める．現在の環境に変数束縛 \(x\) = \(v\) を追加した環境を使って，\(e_2\) の値 \(v_2\) を求める．\(v_2\) がlet式の値となる．拡張した環境は \(v_2\) を求めるため(だけ)には使うが，その後は特に使わないことに注意せよ．
letによる関数定義 (let\(f\)(\(x_1\),\(\ldots\),\(x_n\)) =\(e\);;もしくは let\(f\)(\(x_1\),\(\ldots\),\(x_n\)) =\(e\)in\(e_2\))
トップレベルもしくは現在の環境に，(1)関数のパラメータ名(の列)，(2)本体式，そして(3)\(e\)に現れる \(x_i\) 以外の変数の値で作った環境，の3つを組にしたもの—これを 関数閉包(function closure) と呼ぶ—を \(f\) の値として環境に追加する(そして，\(e_2\) の値を求める．)
変数式 (\(x\))
変数が式の中で使用されている時は，現在の環境からその変数の束縛を探して値を取り出す．この際，探索は新しい束縛から順に行っていく．そのため，同じ変数を何度も宣言した場合は，一番最後のものを使うことになる．
関数呼出し式 (\(f\)(\(e_1\),\(\ldots\),\(e_n\)))
まず，現在の環境を使って \(e_1, \ldots, e_n\) の値 \(v_1, \ldots, v_n\) を求める．(この値を求める順番は，実は特に指定されておらず実装依存である1．) 次に関数 \(f\) の本体式を，\(f\) に格納されている環境に束縛 \(x_1 = v_1, \ldots, x_n = v_n\) を追加したような環境で評価する(\(x_i\)は \(f\)の\(i\)番目のパラメータ変数)．その値が関数呼出し式の値となる． 呼出し側の環境は一旦脇に置いておいて\(f\) が定義された時点での環境を使う，というのがポイントである．これによって静的スコーピングが実現できる．

練習問題

# let pi = 3.14;;
# let area r = let tmp = r *. r in tmp *. pi;;
# let pi = 2;;
# area 5.0;;

の実行過程を上の説明に即して説明せよ．

再帰とスタック・オーバーフロー

上で述べたように，Java ではメソッドの呼出しを一回行う毎にフレームをメモリに確保して，メソッド本体の実行を行い，実行が終了したらそれを解放して，呼出し元に実行を移す．フレームは新しく確保したものから先に解放される，という意味で FIFO の原則に従うため，通常，フレーム管理はスタックを用いて行う．あるメソッドの実行中に，別のメソッド呼出しが発生して，その本体の実行中に，メソッド呼出しが発生して，というように呼出しの段数が増えるとその分だけスタックを消費するわけだが，段数が増えすぎるとスタック領域が足りなくなってプログラムが異常終了することがある．これが スタック・オーバーフロー(stack overflow) である．

また，以下は，Javaで書かれた 1 から \(n\) までの和を計算する簡単な再帰メソッド2だが，手元の環境では引数が 17500 あたりになると，StackOverflowError という例外が発生し，プログラムの実行が異常終了してしまった．

public static int sum(int n) {
  if (n == 1) {
    return 1;
  } else {
    return n + sum(n - 1);
  }
}

public static void main(String[] args) {
  int n = 17500;
  System.out.println("sum(" + n + ") = " + sum(n) + "\n");

  return;
}

実行結果:

Exception in thread "main" java.lang.StackOverflowError
    at RecIter.sum(RecIter.java:6)
    ...

これは OCaml でもCでも同じ事情である．関数の呼び出しを一度行う毎に，本体式を評価するための環境が用意されるため，呼出しの段数が深くなるとスタック・オーバーフローが発生する．以下のOCamlの関数は \(n\) = 260000 を越えたあたりでスタック・オーバーフローが発生した．

# let rec sum n =
    if n = 1 then 1
    else n + sum (n-1);;
val sum : int -> int = <fun> 
# sum 260000;;
- : int = 33800130000
# sum 270000;;
Stack overflow during evaluation (looping recursion?).

C言語でも引数が 270000 になると，OS レベルのエラー (スタック領域をはみだしてメモリの読み書きをしてしまったことで発生した segmentation fault) によって，プログラムの実行が異常終了した．

int sum(int n) {
  if (n == 1) {
    return 1;
  } else {
    return n + sum(n - 1);
  }
}

int main(void) {
  int n = 260000;
  printf("sum(%d) = %d\n", n, sum(n));

  return 0;
}

次は，ユークリッドの互除法で最大公約数を求める関数である．(ただし，再帰呼出しの回数を多くするために，剰余を求めずに，引き算を使っている．)

public static int gcd(int n, int m) {
  if (n == m) { return n; }
  else if (n > m) { return gcd(n-m, m); }
  else /* m > n */ { return gcd(m-n, n); }
}

public static void main(String[] args) {
  int a = 40000;
  int b = 2;
  System.out.println("gcd(" + a + ", " + b + ") = " + gcd(a,b) + "\n");
  return;
}

a, b を上のように設定することで，スタック・オーバーフローが発生した．

しかしながら，OCaml で gcd を定義すると，驚くべきことに(？)引数が大きくなっても sum と違ってスタックオーバーフローが発生する様子がない．これは一体どうしてだろうか．

let rec gcd(n, m) =
  if n = m then n
  else if n > m then gcd(n-m, m)
  else (* m > n *) gcd(m-n, n)
# gcd(540001, 2);;
- : int = 1
# gcd(5400001, 2);;
- : int = 1
# gcd(54000001, 2);;
- : int = 1
# gcd(540000001, 2);;
- : int = 1

末尾呼出しと末尾呼出しの最適化

sum と gcd は，どちらも再帰呼出しを行うものの，再帰呼出しの結果の扱いが違う．すなわち，sum は再帰呼出しの結果に対し足し算を行った値を返す一方で，gcd は，再帰呼出しの結果がそのまま返値となっている．このような，返値の位置にある関数呼出しを---再帰呼出しでも別の関数呼出しでも--- 末尾呼出し(tail call) と呼ぶ．

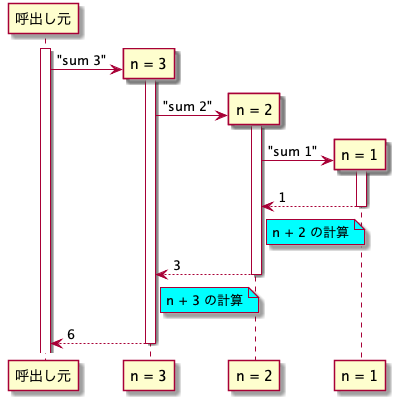
以下，sum の実行の様子をシーケンス図を使って(濫用して？)説明する．ライフラインが，各関数の実行(フレームの生存期間と思ってもよい)を示している．

再帰呼出しが戻ってきてから足し算をして，それから値を返している．

一方，gcd の場合

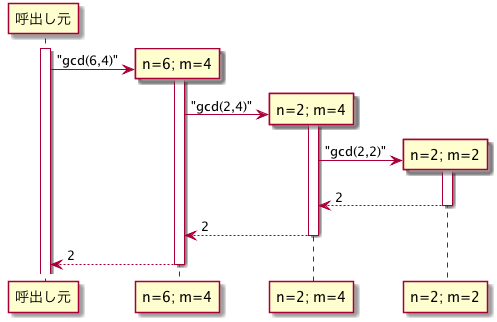
のように，再帰呼出しで得られた値を「たらい回し」で，そのまま呼出し元に返している．

末尾呼出しは，多くの場合，呼出しを行う直前に呼出し側のフレームの領域を解放することができる．このため，末尾呼出しを繰り返す限りにおいてはスタック領域を食いつぶすことなく実行を続けることができる．このように末尾呼出しを特別扱いすることを 末尾呼出しの最適化(tail-call optimization) もしくは 末尾呼出し除去(tail-call elimination) と呼ぶ．OCaml ではこれが実装されており，gcd のように末尾呼出しを繰り返す関数についてはスタック・オーバーフローを起こすことなく実行を続けることができる．C言語では，コンパイラ起動時に -O2 などのオプションをつけて最適化するように指示をすると，末尾呼出しを検知して末尾呼出し最適化を行ってくれるようである．

// C/samples/gcd.c

#include <stdio.h>

int gcd(int n, int m) {
  if (n == m) { return n; }
  else if (n > m) { return gcd(n-m, m); }
  else /* m > n */ { return gcd(m-n, n); }
}

int main(void) {
  int a = 540001;
  int b = 2;
  printf("gcd(%d, %d) = %d\n", a, b, gcd(a, b));
  return 0;
}

というプログラムを，-O2 をつけたり外したりしてコンパイルし，実行結果を比べてみるとよいだろう．(macOSの人は gcc の代わりに clang を使ってください．)

$ gcc -o gcd.out gcd.c
$ gcd.out
Segmentation fault
$ gcc -O2 -o gcd.out gcd.c
$ gcd.out
gcd(540001, 2) = 1

末尾呼出しにおいてフレームの領域を解放できるのはなぜか考えてみよう．関数 f から関数 g を末尾呼出しする直前の状況を考える．f の残りの仕事は g からの返値を f の呼出し元に返すだけなので，多くの場合(OCamlでは必ず)，局所変数の領域はこの時点で必要なくなる．また，フレームには，局所変数の情報だけでなく，関数から返る際に実行をどこへ戻せばよいかの戻り先情報が書かれているが，末尾呼出しの場合，これも以下の工夫をすることで不要になる．f の呼出し元への戻り番地情報は，f から f の呼出し元に値を返す時に必要になるように思えるが，g のフレームに書かれる戻り番地を g の呼出し元(すなわち f の最後)にせず f の呼出し元に(g から f を飛ばして f の呼出し元に直接返るように)するのである．すると，以下の図で示すような呼出し系列が実現できる．gcd の各呼出しで再帰呼出しと同時に，フレームが不要になることをライフラインの幅が太くなくなることで示している．また，最後の再帰呼出しから一気に最初の呼出し元に制御が返ってきている．

末尾再帰関数から繰り返し処理へ

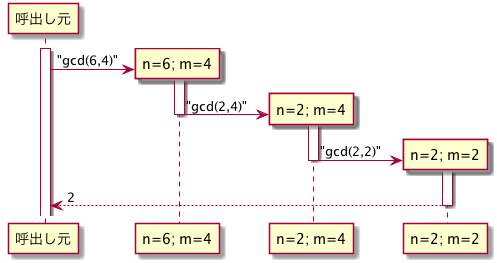
再帰関数定義中の再帰呼出しが全て末尾呼出しになっているような関数を 末尾再帰関数(tail-recursive function) と呼ぶ．gcd は末尾再帰関数である．末尾再帰関数は，系統的な方法で，再帰を使わない，繰り返し構文(と代入)を使った処理に書き換えることができる．

まず，例を見てみよう．Java の gcd メソッドは以下のように書き換えることができる．(この例は，後述する系統的な書き換えを愚直に適用したので無駄な処理が含まれている．)

public static int gcdIter(int n, int m) {
  while (true) {
    if (n == m) { return n; }
    else if (n > m) {
      n = n - m;
      m = m;
    } else /* m > n */ {
      int tmp = n;
      n = m - n;
      m = tmp;
    }
  }
}

書き換えのポイントは以下の通りである．

これで，関数本体が繰り返し実行される．条件式は true なので終了しないようにも思えるが，return 文を実行することで，関数を抜けることになる．再帰呼出しの代わりの代入は，先程述べた，末尾呼出しの最適化，すなわち，末尾呼出し前のフレームの解放・呼出し後の新たなフレームの確保と局所変数の初期化をプログラムで実現しているといえる．

以下は，gcd_iter と，実質的には同じ動作をするが，m = m; のような無駄な代入を省き，while の条件を return 文に到達する条件の否定に変えて，return 文を関数の最後に移動させたバージョンである．

public static int gcdIterTake2(int n, int m) {
  while (n != m) {
    if (n > m) {
      n = n - m;
    } else /* m > n */ {
      int tmp = n;
      n = m - n;
      m = tmp;
    }
  }
  return n;
}

このように末尾再帰関数は繰り返しに帰着させることができる．逆に，繰り返し構文を末尾再帰関数に変換することもできる．繰り返し構文の使用一箇所につき，ひとつ関数定義を用意することになる．

2分探索木の処理でも実はstatic メソッドを使って実装した findは末尾再帰的である．よって，同様の変換を施して繰り返しで書き直すことができる．以下の findIter が，愚直に変換をして得られるバージョン，findIterTake2 が，return するための条件の否定をループの条件にしたり，無駄な代入を省くことで得られるバージョンである．この最後の findIterTake2 は，アルゴリズムの教科書に書かれているであろう定義に非常に近くなっているのが面白いところである．

public static boolean find(BinarySearchTree t, int n) {
    if (t == null) {
        return false;
    } else if (n == t.v) {
        return true;
    } else if (n < t.v) {
        return find(t.left, n);
    } else /* n > t.v */ {
        return find(t.right, n);
    }
}

// 変換を愚直にした繰り返し版
public static boolean findIter(BinarySearchTree t, int n) {
    while (true) {
        if (t == null) {
            return false;
        } else if (n == t.v) {
            return true;
        } else if (n < t.v) {
            t = t.left;
            n = n;
        } else /* n > t.v */ {
            t = t.right;
            n = n;
        }
    }
}

// 無駄を取り除いた繰り返し版
public static boolean findIterTake2(BinarySearchTree t, int n) {
    while (t != null && n != t.v) {
        if (n < t.v) {
            t = t.left;
        } else /* n > t.v */ {
            t = t.right;
        }
    }
    return (t != null);
}

OCaml では，末尾呼出し最適化がされるので，元の gcd や find をそのまま実行すればよい． わけだが，を使えば，代入可能な変数を模倣することができるので，それと(紹介していない) while -- do -- done 構文を組み合わせて同様な変換をすることもできる．

let gcd(n, m) =
  let nv = ref n in
  let mv = ref m in
  while (!nv <> !mv) do
    if (!nv > !mv) then
      nv := !nv - !mv
    else (* !mv > !nv *)
      begin
        let tmp = !nv in
        nv := !mv - tmp;
        mv := tmp
      end
  done;
  !nv

C 言語だと以下のようになる．

bool find(struct tree *t, int n) {
  if (t->tag == LEAF) {
    return false;
  } else /* t->tag == BRANCH */ {
    struct branch b = t->dat.br;
    if (n == b.value) {
      return true;
    } else if (n < b.value) {
      return find(b.left, n);
    } else /* n > b.value */ {
      return find(b.right, n);
    }
  }
}

// 変換を愚直にした繰り返し版
bool find_iter(struct tree *t, int n) {
  while (true) {
    if (t->tag == LEAF) {
      return false;
    } else /* t->tag == BRANCH */ {
      struct branch b = t->dat.br;
      if (n == b.value) {
        return true;
      } else if (n < b.value) {
        t = b.left;
        n = n;
      } else /* n > b.value */ {
        t = b.right;
        n = n;
      }
    }
  }
}

// 少し書き換えてスッキリした版
bool find_iter_take2(struct tree *t, int n) {
  while (t->tag != LEAF && n != t->dat.br.value) {
    struct branch b = t->dat.br;
    if (n < b.value) {
      t = b.left;
    } else /* n > b.value */ {
      t = b.right;
    }
    // or, equivalently, t = (n < b.value) ? b.left : b.right;
  }
  return (t->tag != LEAF);
}

末尾再帰化

さて，冒頭で定義した sum のような関数は末尾再帰関数ではないため，n を大きくするとスタック・オーバーフローを起こしてしまう．しかし，うまいことプログラムを変形することで，末尾再帰関数にすることができる．この章の最後に，いくつかの再帰関数を末尾再帰関数，さらには繰り返し処理へ変形する例を見てみよう．例とするのは sum と mutable な2分探索木の insert である．この時，変形のポイントになるのは，「再帰呼び出しが終わった後の計算を，再帰関数側でやってもらうようにする」ということである．

sum の末尾再帰化

sum の定義をもう一度見てみよう．

let rec sum n =
  if n = 1 then 1
  else n + sum (n-1)

この定義では，sum (n-1) という再帰呼び出しの後，この関数から返るまでに「再帰呼び出しの結果に n を足す」という計算をしており，この部分のせいで末尾再帰でないことがわかる．「再帰呼び出しが終わった後の計算を，再帰関数側でやってもらうようにする」というのは，この足し算の部分を，再帰呼び出しの中でやってもらうようにしよう，というわけである．

これには，まず，sum の引数をひとつ増やして「(本来の)計算が終わった後に何を足せばよいか」を受けとれるように sum(n,m) とする．この第二引数が，上の「再帰呼び出しの結果に n を足す」と対応している．元の sum n は「1からnまでの整数の和」を計算するものだったが，この新しい sum(n,m) は，「1からnまでの和とmの和」となり，次のような定義になる．

let rec sum' (n, m) =
  m + (if n = 1 then 1
       else sum' (n-1, n))

ポイントは，

残念ながらこの定義は，まだ末尾再帰ではない．次に，m + (if ...) に着目してみる．if の場合分けの結果に m を足す，ということは，if の外側の部分を then, else 部それぞれの式に m + を「分配」して押し込んでも結果は変わらないはずである．これにより次の定義を得る．

let rec sum' (n, m) =
  if n = 1 then m + 1
  else m + sum' (n-1, n)

else 部の m + sum' (n-1, n) の値は「『1から n-1 までの和と n の和』とmの和」のはずである．足し算は結合則があるので，これは「1から n-1 までの和と n+m の和」であることに注意すると，再帰呼び出しの第二引数として n の変わりに n+m を渡せば，else 部の m + が除去できることがわかる．この結果得られるのが次の定義である．

let rec sum'' (n, m) =
  if n = 1 then m + 1
  else sum'' (n-1, m + n)   (* tail recursive! *)

これは末尾再帰になっている! ただし，この sum'' を使って 1 から n までの和を計算したい場合は sum''(n, 0) と第二引数に 0 を渡さないといけないので少々注意が必要である．

同じ変形は Java のsumの定義でもできて，以下のような定義が得られる．

public static int sum2(int n, int m) {
  if (n == 1) then {
    return m + 1;
  } else {
    return sum2(n-1, m + n);
  }
}

これを，上と同じように(ほとんど)機械的に繰り返しを使った定義に書き換えると以下のような関数定義になる．

public static int sum2Iter(int n, int m) {
  while (n != 1) {
    m = m + n;
    n = n - 1;
  }
  return m + 1;
}

もしも，この関数を呼ぶ時は必ず m を 0 として呼ぶのであれば，

public static int sum2Iter(int n) {
  int m = 0;
  while (n != 1) {
    m = m + n;
    n = n - 1;
  }
  return m + 1;
}

としてもよい．この定義は，Java(やC言語)プログラムとしては，かなりオーソドックスな「0 から n まで足す」プログラムの書き方である．(多くの人は，n をカウントダウンする代わりに，別にカウンタを用意して 1 から n までカウントアップする定義を書くかもしれないが．)

この変形のポイントは，最初に書いた通り，「再帰呼び出しが終わった後の計算を，再帰関数側でやってもらうようにする」ということである．また，一旦，m + sum' (n-1, n) を得た後，(足し算の結合則を利用して) sum''(n-1, m + n) を導いているのは，いわば「再帰呼び出しが終わった後の計算を合成」しているわけである．

C言語で同じことをすると以下のようになる．

int sum2(int n, int m) {
  if (n == 1) then { return m + 1; }
  else { return sum2(n-1, m + n); }
}

int sum2_iter(int n, int m) {
  while (n != 1) {
    m = m + n;
    n = n - 1;
  }
  return m + 1;
}

int sum2_iter(int n) {
  int m = 0;
  while (n != 1) {
    m = m + n;
    n = n - 1;
  }
  return m + 1;
}

(mutable版) insert の末尾再帰化

短命な2分探索木の挿入操作(と，おそらく削除操作)は，C言語の機能を活かすと，同じ考えを応用することで末尾再帰化することができる．

C 言語版

まず，元の定義を再掲する．

struct tree *insert(struct tree *t, int n) {
  if (t->tag == LEAF) {
    free(t);
    return newbranch(newleaf(), n, newleaf());
  } else /* t->tag == BRANCH */ {
    struct branch *b = &(t->dat.br);
    if (n == b->value) {
      return t;
    } else if (n < b->value) {
      struct tree *newleft = insert(b->left, n);
      b->left = newleft;
      return t;
    } else /* n > b->value */ {
      struct tree *newright = insert(b->right, n);
      b->right = newright;
      return t;
    }
  }
}

再帰呼び出しは10行目，14行目の二箇所あるが，再帰呼び出しから返ってきた後にやっていることは，

となっている．(以下，10行目の再帰呼び出しに注目するが，もうひとつも同様にできる．)この newleft は読みやすさのために導入しただけで，実は

      b->left = insert(b->left, n);

と書いてもよかったものである．この，「b->left へ代入し」の部分を再帰呼び出し側でやってもらうことにしよう．これを行うためには b->left のアドレス &b->left を再帰呼び出しで渡してあげればよい．(& が必要なことに注意せよ．)b->left の型は struct tree * なので，そのアドレスは struct tree ** (tree構造体へのポインタへのポインタ) という型で表される．insert の引数を増やして書き換えた結果が以下の定義である．

struct tree *insert2(struct tree *t, int n, struct tree **pt) {
  if (t->tag == LEAF) {
    free(t);
    struct tree *newt = newbranch(newleaf(), n, newleaf());
    *pt = newt; /** Attention! **/
    return newt;
  } else /* t->tag == BRANCH */ {
    struct branch *b = &(t->dat.br);
    if (n == b->value) {
      *pt = t; /** Attention! **/
      return t;
    } else if (n < b->value) {
      insert2(b->left, n, &b->left);
      *pt = t; /** Attention! **/
      return t;
    } else /* n > b->value */ {
      insert2(b->right, n, &b->right);
      *pt = t; /** Attention! **/
      return t;
    }
  }
}

pt が増えた引数で，この関数は return する前に返値を pt の指す先に代入することになる．(コメントで /** Attention! **/ と書いた4箇所．)また，再帰呼び出しの結果は使わないので，insert2(...); と結果を捨てるように呼び出している．

次に，

ということに注目し，さらにプログラムを書き換えると以下の insert3 が得られる．

// Values returned from insert2 are not really used. So, let's change the return type to void.
// If this function is always called with *pt == t, the assignment *pt = t is nop.  Indeed, 
// this relation holds at all recursive calls.  So, if the first, top-level call ensures
// t == *pt, we can remove *pt = t;.
void insert3(struct tree *t, int n, struct tree **pt) {
  if (t->tag == LEAF) {
    free(t);
    *pt = newbranch(newleaf(), n, newleaf());
    return;
  } else /* t->tag == BRANCH */ {
    struct branch *b = &(t->dat.br);
    if (n == b->value) {
      return;
    } else if (n < b->value) {
      insert3(b->left, n, &b->left);
      return;
    } else /* n > b->value */ {
      insert3(b->right, n, &b->right);
      return;
    }
  }
}

これは，再帰呼び出しの直後に return しているので末尾再帰であり，以下のような繰り返しを用いた定義に書き換えることができる．

void insert_iter(struct tree *t, int n, struct tree **pt) {
  while (true) {
    if (t->tag == LEAF) {
      free(t);
      *pt = newbranch(newleaf(), n, newleaf());
      return;
    } else /* t->tag == BRANCH */ {
      struct branch *b = &(t->dat.br);
      if (n == b->value) {
        return;
      } else if (n < b->value) {
        t = b->left;
        n = n;
        pt = &b->left;
      } else /* n > b->value */ {
        t = b->right;
        n = n;
        pt = &b->right;
      }
    }
  }
}

さらに，while の条件式を，return する条件の否定にして，ループを出てから return するよう書き換えたのが以下の定義である．ついでに n = n; のような無駄な代入も除去している．

void insert_iter_take2(struct tree *t, int n, struct tree **pt) {
  while (t->tag != LEAF && n != b->value) {
    struct branch *b = &(t->dat.br);
    if (n < b->value) {
      t = b->left;
      pt = &b->left;
    } else /* n > b->value */ {
      t = b->right;
      pt = &b->right;
    }
  }
  if (t->tag == LEAF) {
    free(t);
    *pt = newbranch(newleaf(), n, newleaf());
  }
  return;
}

この定義は，C言語でアルゴリズムの解説をしている教科書にある，典型的な挿入操作の定義とほぼ同じになっている．

Javaだとどうなる？

null ポインタを使い，static メソッドで各処理を実装した２分探索木の定義に同じアイデアを適用すれば， Java でも同様な末尾最適化ができそうに思うかもしれない．しかし，これはうまくいかない． Java にはC言語の &b->left のような，構造体の途中を指すポインタを作る機能がないためである．

OCaml は？

(未執筆) --- [ 前の資料 | 講義ホームページ・トップ | 次の資料 ]

  1. といっても，実装がひとつしかないのだが…その唯一の実装では，今のところ，右から左の順で計算される．(が，その順番が将来にわたって保証されているわけではない．)↩︎

  2. n*(n-1)/2 を返せばいいじゃないか，とか言わないでくださいね．↩︎

Copyright 五十嵐 淳, 2016, 2017, 2018, 2019, 2020