[ 講義ホームページ・トップ | 次の資料 ]

2分探索木

今後しばらく使う例題として 2分探索木(binary search tree) をとりあげる．2分探索木はデータ構造の表現，操作の実現方法に様々なバリエーションが考えられるため，複数の言語間の比較だけでなく，ひとつの言語内での機能の比較にもよい例題になる．まずは，2分探索木について抽象的な(プログラミング言語に依存しない)アルゴリズムのレベルでの復習から始めよう．

2分木

以下の規則で構成されるものを 2分木(binary tree) という．

• leafは2分木である．
• 2分木 \(t_1\), \(t_2\) と整数 \(i\) に対し branch(\(t_1\),\(i\),\(t_2\)) は2分木である．

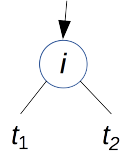
leaf と branch(\(t_1\),\(i\),\(t_2\)) はそれぞれ以下のように図示する．

leaf	branch(\(t_1\),\(i\),\(t_2\))

2分木の例

\(t_a =\) branch(leaf, 10, leaf)

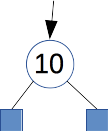
\(t_b =\) branch(\(t_a\), 15, branch(leaf, 25, leaf)) (\(=\) branch(branch(leaf, 10, leaf), 15, branch(leaf, 25, leaf)))

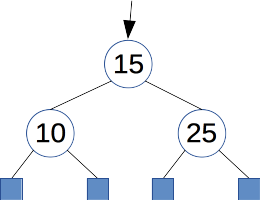
また，図を書く時には leaf の部分をしばしば省略する．

\(t_c =\) branch(\(t_b\), 40, branch(branch(leaf, 50 leaf), 65, leaf))

補足

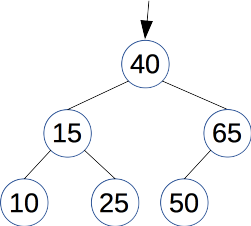
leaf (葉)は子を持たないノード，branch は整数を格納したふたつの子(部分木)を持つノードを表している．一番外側の branch が根に相当する．2分木はグラフの特別な場合として定義されることも多い(グラフ理論ではむしろその方が標準的な定義である)が，実質，等価な定義になっていることを確認してもらいたい．(leaf の存在を無視してしまうのが重要である．)

また，この定義は再帰的である．すなわち，2分木の定義中に再び2分木が言及されている．しかし，leafの項については言及されていないので，これを種にしてより大きな2分木を構成していくことができる．また，2分木の構成法は 上に書かれた二種類しかない ので，以下のようなことがいえる．

任意の2分木\(t\)について，

• \(t\) = leaf または
• ある2分木 \(t_1, t_2\) と整数 \(i\) が存在して \(t\) = branch(\(t_1\),\(i\),\(t_2\))

が成立する．

このことは，当たり前のようだが， 2分木に対する処理を考える時には，基本的には leaf と branch のふたつの場合さえ考えればよい ，という意味で重要である．

2分木上の関数

2分木上の関数の例として，木のサイズ(branch の数)を表す \(size(t)\) と，深さ(根から各葉までに通過するbranchの数の最大)を表す \(depth(t)\) を考えてみよう．

具体例

\(size(t_a) = 1\) \(size(t_b) = 3\) \(size(t_c) = 5\)

\(depth(t_a) = 1\) \(depth(t_b) = 2\) \(depth(t_c) = 3\)

\(size\), \(depth\) の(再帰的)定義

\(size(\)leaf\() = 0\) \(size(\)branch(\(t_1\), \(i\), \(t_2\))\()\) = \(size(t_1) + size(t_2) + 1\)

\(depth(\)leaf\() = \fbox{ ?? }\) \(depth(\)branch(\(t_1\), \(i\), \(t_2\))\() = \fbox{ ?? }\)

2分木が再帰的に定義されているため，2分木上の関数は 自然に 再帰的に定義されることになる¹．

2分探索木

2分探索木(binary search tree) は，大小関係があるようなデータ(正確には全順序集合)の集まりを表すためのデータ構造で，要素の 探索(find) ， 追加(insert) ， 削除(delete) 操作を行うことができる．2分探索木は，節点に格納されたデータ(ここでは整数)が以下の条件を満たすような特殊な2分木である．

任意の branch(\(t_1\),\(i\),\(t_2\)) について，部分木 \(t_1\) に現れる任意の整数 \(j\) について \(j < i\) かつ，部分木 \(t_2\) に現れる任意の整数 \(k\) について \(i < k\) が成立する．

この条件のおかげで，木がバランスしている場合の探索は効率よく行うことができる．一方で，追加・削除にあたってはこの条件を崩さないように木の形を維持する必要があるので少しややこしい．(さらに，バランスを保つように挿入・削除のアルゴリズムを工夫したものがAVL木や赤黒木といったデータ構造であるが，この講義では扱わない．)

ここでは，2分探索木は2分木の特殊な場合として与えているが，2分木を定義した時と同様に，その構成規則を与えることで定義することもできる²．

2分探索木の例

既に例でみた \(t_a, t_b, t_c\) はみな2分探索木になっている．

探索

探索は以下のような簡単な再帰手続きで与えることができる．

find(t, i)  // t is a tree and i is an integer; find returns a Boolean.
  if t is leaf then return false
  else if t is branch(t1, j, t2) then
    if i = j then return true
    else if i < j then return find(t1, i)
    else return find(t2, i)

2分探索木の条件より，根に格納された整数と探索する整数の大小関係によって，どちらかの部分木は探索対象から外すことができるというのがミソである．

挿入

挿入に際しては，探索と同様な要領で木にもぐっていき，葉に辿りついたらそれを新しい節点で置き換えることになる．

insert(t, i)  // t is a tree and i is an integer
  if t is leaf then replace t with branch(leaf, i, leaf) and return
  else if t is branch(t1, j, t2) then
    if i = j then return
    else if i < j then insert(t1, i)
    else insert(t2, i)

上の擬似コードでは replace などとさらっと書いているが，後述するように，この部分を実現するのは少し面倒なことが多い．

削除

削除については，まず探索と同様の要領で削除対象の節点を見つけるが，その節点が子をいくつ持つかで処理が変わってくる．

1. 子を持たない節点 branch(leaf,\(j\), leaf) の場合は，これを葉に置き換える．
2. 子がひとつの節点 branch(\(t'\),\(j\), leaf) もしくは branch(leaf,\(j\),\(t'\)) の場合は，この節点を \(t'\) で置き換える．
3. 子がふたつの場合，右の部分木(この要素はみな \(j\) より大きい)の最小値 \(k\) で \(j\) を置き換えるとともに，右の部分木から \(j\) を(再帰的に)削除する．

delete(t, i)  // t is a tree and i is an integer
  if t is leaf then return // do nothing
  else if t is branch(t1, j, t2) then
    if i = j then
      if both t1 and t2 are leaves then replace t with leaf // case 1
      else if t1 is leaf then replace t with t2  // case 2
      else if t2 is leaf then replace t with t1  // case 3
      else let k = min(t2);
           replace j in t with k;
           delete(t2, k);
    else if i < j then delete(t1, i)
    else delete(t2, i)

練習問題: 探索・挿入・削除の再帰的定義

\(find(\)leaf\(, i) = \textit{false}\) \(find(\)branch(\(t_1\), \(j\), \(t_2\)), \(i)\) = \(\left\{\begin{array}{ll} \textit{true} & (\text{if } i=j) \\ find( \fbox{ ?? }, i) & (\text{if } i > j) \\ find( \fbox{ ?? }, i) & (\text{if } i < j) \end{array}\right.\)

\(insert(\)leaf\(, i)\) = branch(leaf, \(i\) ,leaf) \(insert(\)branch(\(t_1\), \(j\), \(t_2\)), \(i)\) = \(\left\{\begin{array}{ll} \fbox{ ?? } & (\text{if } i=j) \\ ...insert(t_2, i)... & (\text{if } i > j) \\ ...insert(t_1, i)... & (\text{if } i < j) \end{array}\right.\)

\(delete(\)leaf\(, i)\) = leaf \(delete(\)branch(\(t_1\), \(j\), \(t_2\)), \(i)\) = \(\left\{\begin{array}{ll} \fbox{ ?? } & (\text{if } i=j) \\ ...delete(t_2, i)... & (\text{if } i > j) \\ ...delete(t_1, i)... & (\text{if } i < j) \end{array}\right.\)

[ 講義ホームページ・トップ | 次の資料 ]

Copyright 五十嵐 淳, 2016, 2017, 2018, 2019, 2020