2019年度「プログラミング言語」配布資料 (6)

Java の2分探索木プログラムでは，ある種類のデータに関する処理が全てひとつのクラスにまとまっているために，例えば木のノードの種類を追加したい場合には，既存のプログラムに修正を加えることなく新たなクラスを定義するだけで済む．一方で，操作単位で見てみると，定義が複数のクラスに散らばっているために見通しが悪い．これは，ノードの種類を追加するには既存のデータ構造定義を修正する必要がある一方で，新しい操作を加えるには単に新しい関数定義を追加するだけで済んだOCamlやCのプログラムとは対照的である．Java で操作が散らばらないようにプログラムを記述するひとつの方法としては，isLeaf などのメソッドや instanceof 演算子を使ってデータの種類についての場合分けを行って記述することが考えられる．

ここで紹介する，ビジターパターン¹は，動的ディスパッチを活用しながら，データに対する操作をデータ定義から分離してプログラムを構成する方法である．find などの2分木に対する操作は，

ということにしてプログラムを組んでいた．ビジターパターンでは，データ構造に対する操作を表すビジターと呼ばれるオブジェクトを用意し，

find 操作のビジターによる定義

文章で書くだけではわかりにくいので，find 操作の例を見てみよう．まず，インターフェースには，これまでと違い accept というメソッドだけが宣言されている．そして引数は Find 型となっている．これが，これから定義する find 操作を表すビジターのクラス名である．

public interface BinarySearchTree {
    boolean accept(Find v);
}

public class Find {
    private int n;

    public Find(int n) {
        this.n = n;
    }

    public boolean caseLeaf() {
        return false;
    }

    public boolean caseBranch(BinarySearchTree left, int v, BinarySearchTree right) {
        if (n == v) {
            return true;
        } else if (n < v) {
            return left.accept(this);
        } else /* n > v */ {
            return right.accept(this);
        }
    }
}

caseLeaf と caseBranch というメソッドがあって，この中身は葉の場合の処理，枝の場合の処理がほぼそのままコピーされている．また，探索する整数 n は，Find クラスのインスタンス変数として宣言されている．このFind クラスのオブジェクト，例えば new Find(5) は「5 を探索する操作」を表すオブジェクトとして機能する．2分木に対して探索をしたい場合には，以下のように accept メソッドの引数として Find オブジェクトを渡すことになる．

BinarySearchTree t = ...;
boolean b = t.accept(new Find(5));  // Does t store 5?

さて，上のように accept を呼ぶと，t が Leaf か Branch いずれかの accept メソッドを呼ぶことになる．仕上げは，それぞれの accept メソッドから，引数として渡された Find オブジェクトに対し caseLeaf または caseBranch を呼ぶように Leaf と Branch を定義することにある．

public class Leaf implements BinarySearchTree {
    public Leaf() {
    }

    public boolean accept(Find visitor) {
        return visitor.caseLeaf();
    }
}

public class Branch implements BinarySearchTree {
    private BinarySearchTree left;
    private int v;
    private BinarySearchTree right;

    public Branch(BinarySearchTree left, int v, BinarySearchTree right) {
        this.left = left;
        this.v = v;
        this.right = right;
    }

    public boolean accept(Find visitor) {
        return visitor.caseBranch(left, v, right);
    }
}

6行目と22行目が肝である．受け取った visitor に対し，Leaf クラスでは caseLeaf を，Branch クラスでは caseBranch を呼ぶことで，葉・枝それぞれに対する処理をするわけである．この際，(枝の場合)インスタンス変数もビジターに渡してあげるのも大事な点である²．

find 操作の動作

さて，このように定義されたプログラムの動作を シーケンス図(sequence diagram) を使って説明しよう．シーケンス図はクラス図と同様に UML 記法のひとつで，複数のオブジェクト間のメソッド呼出しの関係を時系列で示したものである．例えば，

// 呼出し元
BinarySearchTree t1 = new Leaf();
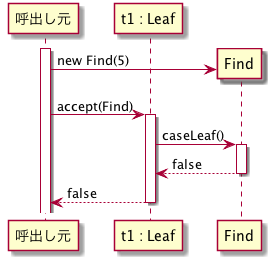
System.out.println(t1.accept(new Find(5))); // should display false

には，t1 (が指す)オブジェクトと Find オブジェクトが登場するが，t1.accept(new Find(5)) の動作を記述したシーケンス図は下のようになる．

図だけ見れば，なんとなく何を意味しているか想像できるかもしれないが，

一方，t1 が Branch である時を考えてみよう．呼出し元のプログラムは以下のようなものを考える．

// Definitions of t3, t4, t5, v1, v2, n, ...
BinarySearchTree t2 = new Branch(t4,v2,t5);
BinarySearchTree t1 = new Branch(t2,v1,t3);
System.out.println(t1.accept(new Find(n)));

ここで，n < v1 が成り立っているとする．すなわち，n の探索は t1 から t2 に続いていく．このプログラムに対するシーケンス図は以下のようになる．

今度は，t1 が Branch なので，accept に続いて Find オブジェクトの caseBranch メソッドが呼出されているのがポイントである．その際，t1 のインスタンス変数がごっそりビジターに渡されて，その中で n と v1 の比較が行われる．次は，左の部分木 t2 に対する(再帰に相当する)呼出しだが，これはビジター内の処理を呼出し元として，再び accept メソッドを呼ぶことで行われる．その結果，t2 に対する accept の呼出しは，再び caseBranch の呼出しとなって戻ってくる．一回目の caseBranch の処理が途中のまま，再び caseBranch が呼出されていることを示すため，ライフラインが二重に太くなっている．この先の処理は n と v2 の大小に依存するが，そこは書いていない．(n と v2 が等しい場合にはすぐに true を返すので必ずしも，accept 呼出しが発生するわけではない．)その後，true か false が決定されたら，それがたらい回しに元来た経路を辿って，呼出し元まで伝播していく．

かなりややこしい経過を辿るが(特に Find のメソッド呼出しの途中で，また Find のメソッドが呼ばれる，というのが，わかりにくいような気がする)，このようにして find 操作が実現でき，かつ，find 操作の本質的な部分を一箇所(すなわち Find クラス)に集めることができた．

ここまでは find 操作に特化したプログラムを書いたが，以下は，このパターンを，色々な操作を同時に使えるように一般化していく．

パターンへの一般化

上にあげたプログラムでは accept メソッドの引数が，特定のクラスである Find に固定されてしまっていたため，探索操作しかできない．一般には色々な操作をビジターとして定義したいわけだが，操作毎に(別の名前の) accept を定義するのでは使い勝手が悪い．そこで，最初の一般化として， boolean を返す操作一般 をうまく扱えるようにする．そのために，ビジターのためのインターフェースを定義し，Find (や，その他 boolean を返すビジターのクラス) はそのインターフェースを implements して定義するようにする．

インターフェース間の矢印は相互に依存関係があることを示している(「矢じり」が，implements を表すものと違うことに注意)．BSTVisitorB が「booleanを返す2分木に対する操作一般」を表すためのインターフェースであり，accept メソッドも Find 決めうちではなく，BSTVisitorB を引数としている．Find は BSTVisitorB を implements する形で定義するため，accept に渡すことができる．他にも BSTVisitorB を implements したクラスを追加する(caseLeaf と caseBranch の具体的な定義を与える)ことで，2分木に対する操作を， 既存のクラスの変更をすることなく 追加することができる．

ここまで一般化すると「パターン」と呼ぶにふさわしくなってくる．

返り値の違うビジターの扱い

上の方法で，boolean を返す操作については一般的に扱うことができるが，他の型(例えば挿入・削除のように2分木や min のように int)を返す操作を追加する場合は，別のインターフェースを用意する．

配布しているソースコードは，この方針で定義されている．クラス・インターフェースの数はかなり増えてしまうが，例えば Insert クラスに書かれていることは，本質的に OCaml プログラムの insert 関数と同じことであることがわかるのではないだろうか．

let rec insert(t, n) =
  match t with
    Lf -> Br {left=Lf; value=n; right=Lf}
  | Br {left=l; value=v; right=r} ->
     if n = v then t
     else if n < v then 
       let new_left = insert(l, n) in
       Br {left=new_left; value=v; right=r}
     else (* n > v *)
       let new_right = insert(r, n) in
       Br {left=l;        value=v; right=new_right}

public class Insert implements BSTVisitorBST {
    private int n;
    
    // constructor is omitted

    public BinarySearchTree caseLeaf() {
        return new Branch(new Leaf(), n, new Leaf());
    }

    public BinarySearchTree caseBranch(BinarySearchTree left, int v, BinarySearchTree right) {
        if (n == v) {
            return new Branch(left, v, right);
        } else if (n < v) {
            BinarySearchTree newLeft = left.accept(this);
            return new Branch(newLeft, v, right);
        } else /* n > v */ {
            BinarySearchTree newRight = right.accept(this);
            return new Branch(left, v, newRight);
        }
    }
}

考察

木のノードの種類を増やしたい場合には，ビジターのインターフェースからビジタークラスまで全てにわたって，caseXXX メソッドを増やす必要があり，結局，OCaml のような関数を使った方法と同様に既存コードを修正しないといけない不便さがある．ノードの種類と操作の種類の両方の拡張性を持つように(静的型付言語で)プログラミングできるかという問題は "Expression problem" という名前がつけられ2000年代のプログラミング言語研究のホットトピックであった．Javaだけでもジェネリクスを駆使すればできることが Torgersen の研究によって知られているが，ScalaなどのJavaよりさらに先進的な機構を持つ言語ではわりと簡潔に記述できる．

多相性の導入

ビジターの返り値型多相 (java/bstPolyVisitor/)

BSTVisitorXXX のようなインターフェースを増やさずに様々な返り値型のビジターを扱うためにはジェネリクスを使うとよい．以下のインターフェース BSTVisitor<Result> は，BSTVisitorI と BSTVisitorB と BSTVisitorBST をまとめたものと考えられる．

public interface BSTVisitor<Result> {
    Result caseLeaf();
    Result caseBranch(BinarySearchTree left, int v, BinarySearchTree right);
}

Result をビジターに応じた返り値型で具体化することが想定されている．各ビジタークラスは BSTVisitor<Integer> などを implement して定義することを想定している．例えば，Find クラスは以下のように定義される．

public class Find implements BSTVisitor<Boolean> {
    // instance variable and constructor omitted

    public Boolean caseLeaf() {
        return false;
    }

    public Boolean caseBranch(BinarySearchTree left, int v, BinarySearchTree right) {
        if (n == v) {
            return true;
        } else if (n < v) {
            return left.accept(this);
        } else /* n > v */ {
            return right.accept(this);
        }
    }
}

型パラメータはプリミティブ型で具体化できないため boolean の代わりに Boolean を使っているが，それ以外の変更は implements 節だけである．

次に2分探索木側の変更を見てみよう．まず，BinarySearchTree は以下のようになる．

public interface BinarySearchTree {
    <Result> Result accept(BSTVisitor<Result> v);
}

accept が Result を型パラメータとする多相メソッドとして宣言されており，引数の方が BSTVisitor<Result> となっている．Result がクラスではなく，メソッドの型パラメータになっている理由は，ひとつの木に対し，返値型が異なるビジターが渡される可能性があるためである．もし，Result をクラスの型パラメータとして

public interface BinarySearchTree<Result> {
    Result accept(BSTVisitor<Result> v);
}

のように定義してしまうと，オブジェクト毎に Result が固定されてしまい，その固定した Result を返すビジターしか受け取れなくなってしまう．(木の fold 操作を思い出そう．)accept は多相メソッドなので，accept の呼び出しには(暗黙的に)型引数を指定することになる．例えば，Find 中の

return left.accept(this);

return left.<Boolean>accept(this);

と書かれるものである．これは実引数の this が Boolean を返すようなビジターであることを示している．(より細かくいうと，<Boolean> と指定することで，accept の引数の型は BSTVisitor<Result> の Result を実際に指定された Boolean で具体化した BSTVisitor<Boolean> になる．this の型は Find であるが，implements節に書いたようにこれは BSTVisitor<Boolean> としても使えるので，この呼び出しは適切である．また，accept の返値型は，定義に書いてある Result を具体化した Boolean であると理解できる．)

この BinarySearchTree に対応した Leaf と Branch クラスは素直に定義できる．以下に Branch のみ示す．

public class Branch implements BinarySearchTree {
    private BinarySearchTree left;
    private int v;
    private BinarySearchTree right;

    public Branch(BinarySearchTree left, int v, BinarySearchTree right) {
        this.left = left;
        this.v = v;
        this.right = right;
    }

    public <Result> Result accept(BSTVisitor<Result> visitor) {
        return visitor.caseBranch(left, v, right);
    }
}

２分探索木を作って，メソッド呼び出しを行う Main クラスのコードも変更の必要はない．

要素型の多相性 (java/polyBSTPolyVisitor/)

2分探索木が格納する要素の型を int に固定せず，ジェネリクスを使って多相的にする場合，BinarySearchTree などに要素の型を表す型引数を追加するのはもちろん，ビジターにも要素型を表す型引数を追加することになる．

public interface BinarySearchTree<Elm extends Comparable<Elm>> {
    <R> R accept(BSTVisitor<Elm,R> v);
}

public interface BSTVisitor<Elm extends Comparable<Elm>, R> {
    R caseLeaf();
    R caseBranch(BinarySearchTree<Elm> left, Elm v, BinarySearchTree<Elm> right);
}

型変数の Elm にその上限 Comparable<Elm> が指定されているのは以前と同じ理由である．

その他

短命な2分探索木をビジターパターンで実装することもできる (java/bstVisitorMutable参照)．しかし，ビジターパターンは動的ディスパッチに依存しているので，葉を null ポインタで表現する方法と組み合わせることはできない．

オブジェクト指向言語でのプログラミングイディオムのいくつかはデザインパターン(design pattern)と呼ばれている．デザインパターンには，ここで紹介するビジターパターン以外にも多数あって，講義資料その(2)で導入した，インターフェースとクラスを使ったデータ構造の表現方法もコンポジットパターンと呼ばれている．↩︎
オブジェクトを丸ごとビジターに渡すことも多い(正式なビジターパターンの定義ではそうなっている)が，ここでは他の実装方式との比較をやりやすくするためにインスタンス変数を渡すようにプログラムを書いている．↩︎

2019年度「プログラミング言語」配布資料 (12)

ビジターパターンによる操作とデータの分離 (java/bstVisitor)

find 操作のビジターによる定義

find 操作の動作

パターンへの一般化

返り値の違うビジターの扱い

考察

多相性の導入

ビジターの返り値型多相 (`java/bstPolyVisitor/`)

要素型の多相性 (`java/polyBSTPolyVisitor/`)

その他

ビジターパターンによる操作とデータの分離 (java/bstVisitor)

find 操作のビジターによる定義

find 操作の動作

パターンへの一般化

返り値の違うビジターの扱い

考察

多相性の導入

ビジターの返り値型多相 (java/bstPolyVisitor/)

要素型の多相性 (java/polyBSTPolyVisitor/)

その他

ビジターの返り値型多相 (`java/bstPolyVisitor/`)

要素型の多相性 (`java/polyBSTPolyVisitor/`)